Bagging- intro

 Bagging, that often considered homogeneous weak learners, learns then independently from each other in parallel and combines then fallowing some kind of deterministic averaging process.

Bagging gets its name because it combines Boostrapping and Aggregation to form one ensemble model.

Boostrapping:

This statistical technique consists in generating samples of size 'm' (i.e boostrap samples) from an initial (original) data set of size 'N' by randomly drawing with replacement 'm' observations.

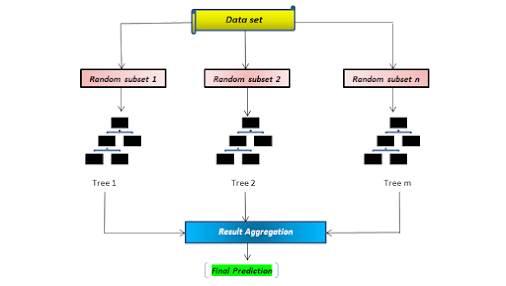
From a given sample of data, multiple boostrapped sub-samples are pulled. A decision tree is formed on each of the boostrapped sub-samples. Then an algorithm is used to aggregate over the Decision trees to form most efficient predictor.

Bagging can perform both classification and regression.

• Classification: Aggregates predictions by majority voting.
• Regression: Aggregates predictions through averaging.

We create multiple boostrap samples so that each new bootstrap will act as another independent data set drawn from true distirbution. Then we can fit a weak learner for each of these samples and finally aggregate them by averaging the outputs.

There are several possible ways to aggregate the multiple models fitted in parallel. For a regression problems, output individual models can be averaged to obtain the output of the ensemble model. For classification problem, we use majority of voting.

 

Pros and cons:

• Bagging takes an advantage of ensemble learning wherein multiple weak learner output perform a single strong learner. It helps to reduce variance and thus helps us avoid over fitting.
• There can be possibly be a problem of high bias if  not modeled properly.

There are many Bagging algorithms of which perhaps the most prominent would be Random Forest.