How does the Decision tree algorithm works ?
Decision tree algorithm is an Greedy approach, based on the concept of Heuristic problem solving by making an optimal local choice at each node. The algorithm fallows the below steps:
- At each stage(node), pick out the best feature as the test condition.
- Now split the node into the possible outcomes
- Repeat the above steps till all the test conditions have been exhausted into leaf nodes.
How to pick the strong condition ??
Decision trees are built using fallowing algorithms:
- CART (Classification And Regression Trees) --> This makes use of Gini impurity as metric
- ID 3 (Iterative Dichotomiser 3) --> This uses entropy and information gain as metric.
Iterative Dichotomiser 3 is one of the most effective algorithm used to build a decision tree. It uses the concept of Entropy and Information gain to generate a decision tree for a given set of data.
Entropy:
In machine learning, entropy is a measure of the randomness in the information being processed. The higher the entropy, the harder it to draw any conclusions from that information.
Information gain can be defined as the amount of information gained about a random variable or signal from observing anther random variable. It can be considered as the difference between the entropy of parent node and weighted average entropy of child nodes.
Gini Impurity :
Gini impurity is a measure of how often a randomly chosen element from the set would be incorrectly labeled if it was randomly labeled according to the distribution of labels in the subset.
Gini impurity is lower bounded by 0, with 0 occurring if the data set contains only one class.
Classification Example using ID 3 algorithm :
Consider weather data set based on which we will determine whether to play football or not ?
Here there are four independent variable to determine the dependent variable. The independent variables are outlook, Temperature, Humidity, and wind. The dependent variable is whether to play football or not.
At the first step, we have to find the parent node for our decision tree. For that follow the steps:
Find the entropy of class variable:
E(S) = - [(9/14) log(9/14) + (5/14) log(5/14)] = 0.94
Note: Here, typically we will take log to base 2. Here total there are 14 Yes/No. Out of which 9 yes and 5 no. Based on it we calculated probability above.
From the above data for outlook we can arrive at fallowing table easily:
No we have to calculate average weighted entropy i.e we have found the total of weights of each feature multiplied by probabilities.
E(S,outlook) = (5/14) * E(3,2) +(4/14)*E(4,0)+(5/14) *E(2,3)
= (5/14) (-(3/5)log(3/5)-(2/5)log(2/5)) + (4/14)(0) + (5/14) ((2/5)log(2/5)-(3/5)log(3/5))
= 0.693.
Next step is to find the information gain. It is the difference between parent entropy and average weighted entropy we found above.
IG ( S,outlook ) = 0.94 - 0.693 = 0.247
Similarly, find information gain for Temperature, Humidity, and Windy.
IG(S, Temperature) = 0.940 - 0.911 = 0.029
IG(S, Humidity) = 0.940 - 0.788 = 0.152
IG(S, Windy) = 0.940 - 0.8932 = 0.048
Now select the feature having largest entropy gain. Here it is Outlook. So, it forms node(root node) of our decision tree. Our data looks as :
Here, our Decision tree is look like :
Next step is to find the next node in our decision tree. Now we will find one under sunny. We have to determine which of the fallowing Temperature, Humidity or Wind has higher information gain(IG).
Calculate parent entropy E(sunny)
E(sunny) = (- (3/5)log(3/5) - (2/5)log(2/5) ) = 0.971
Now calculate information gain of Temperature.
E (sunny.temperature) = (2/5)*E(0,2) + (2/5) * E(1,1) + (1/5)*E(0,1)
= 2/5 = 0.4
IG( sunny,temperature) = 0.971 - 0.4 = 0.571
Similarly we get,
IG(sunny,humidity) = 0.971
IG(sunny,windy) = 0.020
Here, IG (sunny,humidity) is the largest value, so humidity is the node which comes under Sunny.
From this we can say that play will occur if Humidity is normal and will not occur if it is high. Similarly, find the nodes under Rainy
Note: A branch with entropy with more than 0 needs further splitting.
Finally, our Decision Tree will look as below:

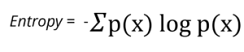










Comments
Post a Comment